科研動(dòng)態(tài)
地下水系統(tǒng)動(dòng)態(tài)模擬中的數(shù)值模型與機(jī)器學(xué)習(xí)模型對比研究.docx
A comparative study among machine learning and numerical models for simulating groundwater dynamics
in the Heihe River Basin, northwestern China
錄用時(shí)間:2020年02月07日
期刊:Scientific Reports(JCR Q1)
作者列表:
1) 陳 沖 (中國石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院)
2) 何 為 (中國石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院 電子信息工程系 博16)
3) 周 涵 (中國石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院 電子信息工程系 研17)
4) 薛亞茹(中國石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院)
5) 朱明達(dá)(中國石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院)
DOI鏈接:https://doi.org/10.1038/s41598-020-60698-9
背景與動(dòng)機(jī):
計(jì)算機(jī)建模已經(jīng)成為各個(gè)自然學(xué)科的研究利器,也是地球系統(tǒng)科學(xué)的基本研究方法。目前,計(jì)算機(jī)模型主要分為經(jīng)驗(yàn)?zāi)P汀?/span>數(shù)值模型與統(tǒng)計(jì)模型。經(jīng)驗(yàn)?zāi)P碗y以模擬動(dòng)態(tài)系統(tǒng);構(gòu)建數(shù)值模型則需要大量的觀測數(shù)據(jù)與專家知識(shí),且難以權(quán)衡模型時(shí)空分辨率與計(jì)算消耗之間的矛盾;基于統(tǒng)計(jì)理論的機(jī)器學(xué)習(xí)模型則較好地解決了以上兩種模型的不足。本研究以地下水系統(tǒng)為例,選擇位于中國西北部的黑河流域作為研究區(qū),對數(shù)值模型與機(jī)器學(xué)習(xí)模型在地下水系統(tǒng)模擬中的構(gòu)建難度、模擬精度等進(jìn)行研究,通過具體的性能指標(biāo)為地下水系統(tǒng)建模中的模型選擇提供依據(jù),同時(shí)也將為其他領(lǐng)域的模型選擇問題提供有益參考。
設(shè)計(jì)與實(shí)現(xiàn):
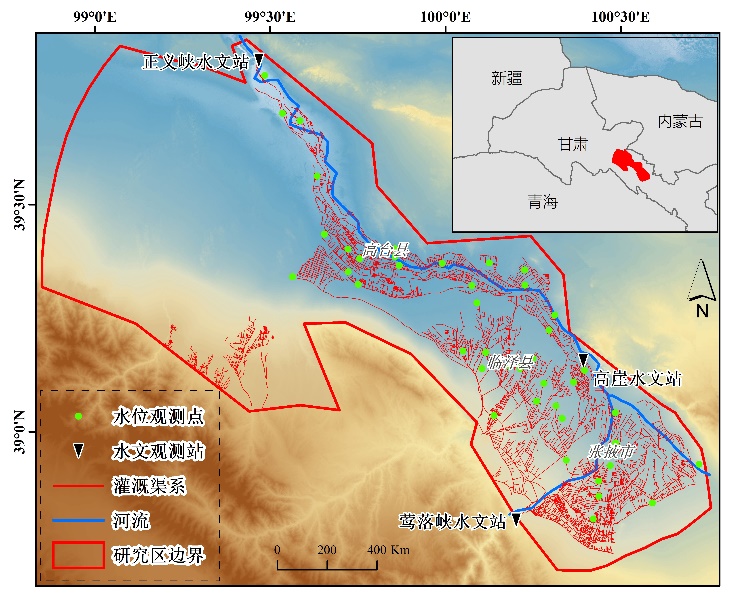
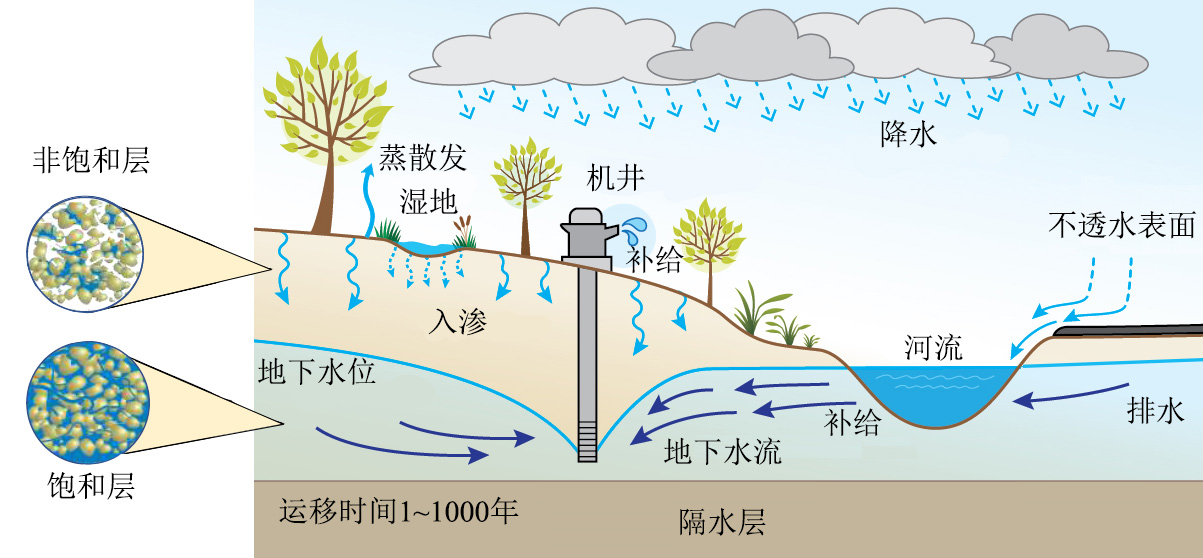
1. 數(shù)據(jù)介紹。黑河流域位于我國西北部干旱區(qū),是我國第二大內(nèi)陸河流域,中游(38°38’N—39°53’,98°53’E—100°44’E;)為典型的干旱氣候,年降水量稀少(69~216 mm),蒸發(fā)強(qiáng)(1453~2351 mm),是黑河流域經(jīng)濟(jì)和農(nóng)業(yè)最發(fā)達(dá)的地區(qū),全國最大的玉米制種基地。中游(見圖1 (a))內(nèi)主要河流有黑河干流與梨園河,鶯落峽、正義峽水文站分別為黑河干流上下游分界點(diǎn)。研究者通過觀測地下水位以及地表河流流量以認(rèn)識(shí)地下水系統(tǒng)在驅(qū)動(dòng)因素的影響下的動(dòng)態(tài)變化,影響地下水系統(tǒng)動(dòng)態(tài)變化的因素主要有自然因素(上游徑流下泄、地下地表水交換、植物蒸散發(fā)、降水、南邊界入流)和人類活動(dòng)因素(抽水變化導(dǎo)致的地下地表水交換增加、地表植被的變化導(dǎo)致的蒸散發(fā)不同),地下水系統(tǒng)循環(huán)過程見圖1 (b)。
(a) (b)
圖1. (a) 黑河流域中游;(b) 地下水系統(tǒng)循環(huán)過程
2. 方法介紹。分別采用機(jī)器學(xué)習(xí)模型與數(shù)值模型構(gòu)建黑河流域中游地下水系統(tǒng)模型。機(jī)器學(xué)習(xí)方法選擇多層感知機(jī)(Multi-layer perceptron)、徑向基網(wǎng)絡(luò)(Radial basis function network)與支持向量機(jī)(Support vector machine)等典型方法;數(shù)值模擬則選擇MODFLOW(Modular Three-dimensional Finite-difference Ground-water Flow Model)構(gòu)建地下水系統(tǒng)模型。
3. 實(shí)驗(yàn)結(jié)果。對模型計(jì)算時(shí)間、模擬精度、預(yù)測精度以及模型的泛化能力進(jìn)行評價(jià)(見表1、表2與圖2)。經(jīng)過對比發(fā)現(xiàn),相比于數(shù)值模型,機(jī)器學(xué)習(xí)模型消耗了更少的計(jì)算時(shí)間得到了更優(yōu)的模擬精度與預(yù)測精度;而數(shù)值模型的泛化能力優(yōu)于機(jī)器學(xué)習(xí)模型。因此,機(jī)器學(xué)習(xí)模型適用于對實(shí)時(shí)性要求高、需要多次運(yùn)行模型且不必考慮物理機(jī)制的情景(如實(shí)時(shí)模型、敏感性分析、不確定性分析、優(yōu)化等)。
表1. 校正/訓(xùn)練期指標(biāo)對比
Numerical model |
MLP model |
RBF model |
SVM model |
||
RMSE |
Groundwater level (m) |
5.61 |
0.99 |
0.84 |
0.83 |
Streamflow rates (m3) |
1.76×106 |
1.09×106 |
1.16×106 |
1.16×106 |
|
R2 |
Groundwater level |
0.52 |
0.71 |
0.75 |
0.76 |
Streamflow rates |
0.51 |
0.66 |
0.66 |
0.66 |
|
Time |
Calibration |
months |
days |
days |
days |
Computation |
1898 s |
716.9 s |
4.2 s |
1.0 s |
|
表2. 預(yù)測期指標(biāo)對比
|
Numerical model |
MLP model |
RBF model |
SVM model |
|
RMSE |
Groundwater level (m) |
5.84 |
1.69 |
1.12 |
1.71 |
Streamflow rates (m3) |
2.05×106 |
1.69×106 |
1.21×106 |
1.17×106 |
|
R2 |
Groundwater level |
0.51 |
0.66 |
0.71 |
0.65 |
Streamflow rates |
0.50 |
0.54 |
0.79 |
0.83 |
|
Time (s) |
30 |
0.07 |
0.06 |
0.10 |
|
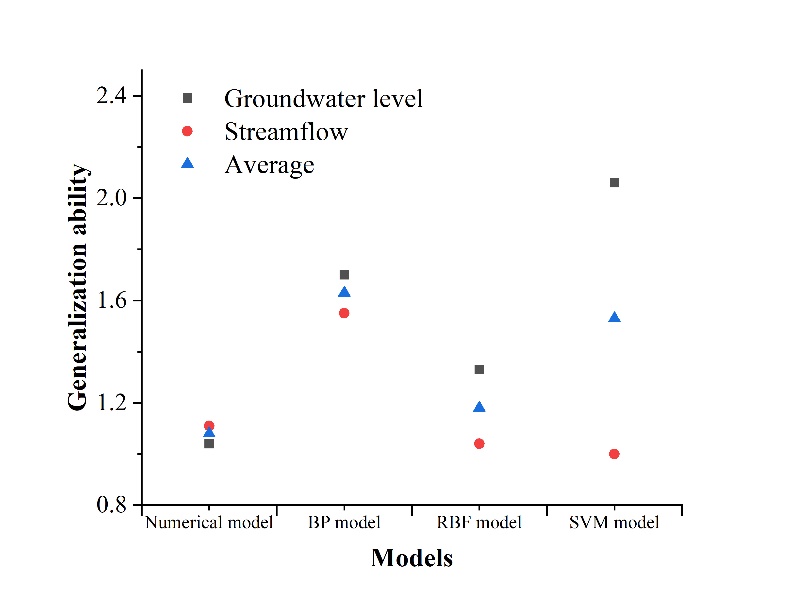
圖2. 不同模型泛化能力對比

