無向圖最小支配集的量子算法及線路設(shè)計
中文題目:無向圖最小支配集的量子算法及線路設(shè)計
論文題目:Quantum algorithm for minimum dominating set problem with circuit design
錄用期刊/會議:Chinese Physics B (中科院大類四區(qū),JCR Q2)
原文DOI:10.1088/1674-1056/ad02e5
原文鏈接:https://iopscience.iop.org/article/10.1088/1674-1056/ad02e5/meta
作者列表:
1)張皓穎 中國石油大學(xué)(北京)人工智能學(xué)院 計算機(jī)科學(xué)與技術(shù) 碩21
2)王紹軒 中國石油大學(xué)(北京)人工智能學(xué)院 計算機(jī)科學(xué)與技術(shù) 碩21
3)劉新建 中國石油大學(xué)(北京)人工智能學(xué)院 計算機(jī)科學(xué)與技術(shù) 碩21
4)沈穎童 中國石油大學(xué)(北京)人工智能學(xué)院 計算機(jī)科學(xué)與技術(shù) 碩22
5)王玉坤 中國石油大學(xué)(北京)人工智能學(xué)院 計算機(jī)科學(xué)與技術(shù)系 教師
文章簡介:
本文提出了一種求解無向圖最小支配集問題的量子算法,該問題是一個著名的NP完全問題,對于圖論和組合優(yōu)化領(lǐng)域具有重要意義。文章整體通過量子算法獲得極小支配集,通過經(jīng)典后處理獲得最小支配集。本文所提出的算法利用Grover搜索算法的特性,通過設(shè)計特定的量子門和電路結(jié)構(gòu)來識別非有向圖中的最小支配集。由于最小支配集問題的解的數(shù)量未知,直接應(yīng)用原始的Grover搜索算法面臨挑戰(zhàn)。為了解決這一問題,文章引入了一種交換測試方法來估計所需的迭代次數(shù)。這為利用Grover算法求解任意目標(biāo)解數(shù)量未知問題提供了方向。
本文主要研究了在無向圖中尋找最小支配集的NP完全問題。為了加快搜索過程,提出了一種基于Grover搜索的支配集搜索算法。然而,利用該方法直接解決最小支配集問題面臨一個困難,即無法精確獲得算法的迭代次數(shù),這使得直接使用原始的Grover的搜索不可能。因此,引入了一種SWAT-TEST方法來確定所需的迭代次數(shù)。算法的查詢復(fù)雜度為O (1.414n),空間復(fù)雜度為O (n)。為了驗證所提出的方法,我們采用qiskit軟件包對量子電路進(jìn)行了模擬,得到了預(yù)期的結(jié)果。
通過對支配集的性質(zhì)進(jìn)行分析,我們將量子比特按照不同的功能分為了7類,并將算法分為支配集探測和極小支配集探測兩個部分,設(shè)計了如圖1所示的量子線路總體框架。
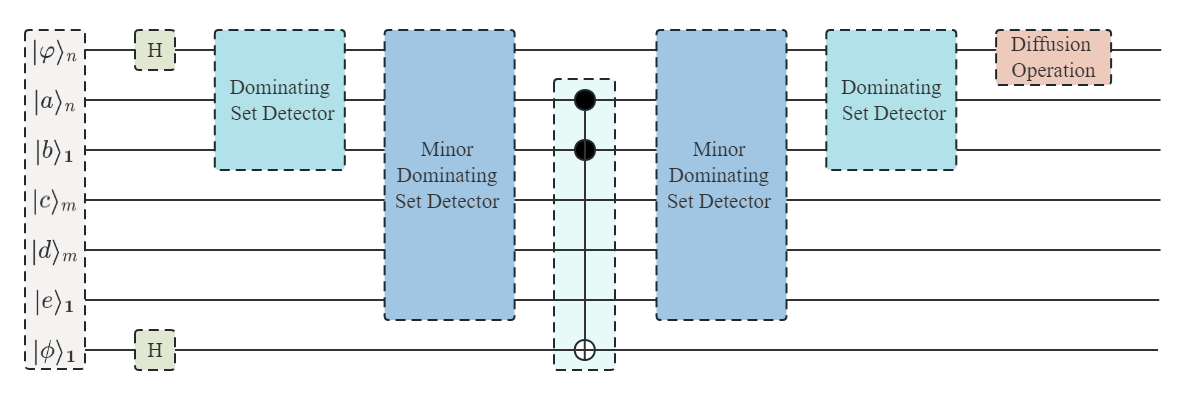
圖1 量子線路框架
支配集探測的核心思想是檢測圖中的每個頂點(diǎn)能否被支配。判斷該頂點(diǎn)及其所有鄰接點(diǎn)中是否存在支配點(diǎn)。極小支配集探測模塊的核心思想是首先判斷頂點(diǎn)在成為非支配點(diǎn)后是否仍然能夠被支配,然后判斷頂點(diǎn)成為非支配點(diǎn)后,其所有鄰接點(diǎn)是否能被支配。然后我們將判斷的思想映射到量子線路中。
我們對3個頂點(diǎn)2條邊的無向圖進(jìn)行了實驗,所設(shè)計的量子線路如圖2所示。其中包括支配集探測、極小支配集探測和反演算子三部分。當(dāng)運(yùn)行完此量子線路之后,可以通過測量量子比特的狀態(tài)來確定極小支配集的組合,然后借助經(jīng)典算法找到最終的解。

圖2 三頂點(diǎn)量子線路
模擬結(jié)果如圖3所示,橫坐標(biāo)表示量子態(tài),對應(yīng)到無向圖的頂點(diǎn)集合,縱坐標(biāo)表示該量子態(tài)被測量得到的概率。算法執(zhí)行完畢后,以高概率獲得兩個極小支配集。通過Grover量子搜索算法獲取所有的極小支配集后,利用經(jīng)典算法在這些集合中進(jìn)行最小支配集的搜索,最終發(fā)現(xiàn){A}是最小的支配集。
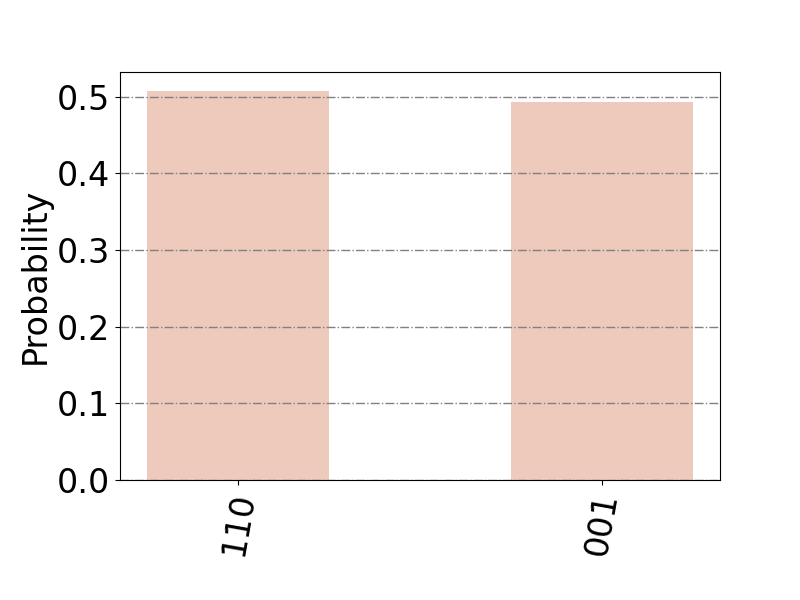
圖3 實驗結(jié)果
我們提出了一種利用Grover的搜索算法來解決在無向圖中尋找最小支配集的問題,該算法相對經(jīng)典的窮舉算法產(chǎn)生了平方級的加速。為了展示整個算法的有效性和效率,我們使用Python和IBM開發(fā)的qiskit包進(jìn)行了模擬。實驗展示了算法在具有3個和8個頂點(diǎn)的無向圖上的性能,展示了該算法在獲得高概率的次要支配集方面的準(zhǔn)確性。隨后,采用經(jīng)典的后處理方法將這些次要支配集轉(zhuǎn)化為最小支配集,顯著減少了搜索空間,并在短時間內(nèi)實現(xiàn)了精確解。
王玉坤,女,博士,人工智能學(xué)院計算機(jī)系助理教授。研究方向為量子計算,量子密碼及量子信息基本理論,主要包括:量子機(jī)器學(xué)習(xí),經(jīng)典困難問題量子算法加速,量子線路優(yōu)化與映射,量子密碼協(xié)議設(shè)計及安全性證明,設(shè)備不可信量子信息處理等。主持國家自然基金青年基金,密碼管理局密碼科技國家重點(diǎn)實驗室面上項目,校人才啟動基金,在國內(nèi)外著名期刊和會議發(fā)表SCI檢索的學(xué)術(shù)論文30余篇。擔(dān)任多個國際頂級期刊審稿人。

