論文題目：Segmented Merge: A New Primitive for Parallel Sparse Matrix Computations

發(fā)表會(huì)議：The 17th Annual IFIP International Conference on Network and Parallel Computing (CCF C類(lèi)會(huì)議)

作者列表

1) 戢昊男 中國(guó)石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)專(zhuān)業(yè) 研20級(jí)

2) 盧世博 中國(guó)石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)專(zhuān)業(yè) 本16級(jí)

3) 侯凱希 美國(guó)弗吉尼亞理工大學(xué)

4) 汪 浩 美國(guó)俄亥俄州立大學(xué)

5) 劉偉峰 中國(guó)石油大學(xué)(北京) 信息科學(xué)與工程學(xué)院 計(jì)算機(jī)科學(xué)與技術(shù)系

6) Brian Vinter 丹麥奧胡斯大學(xué)

文章摘要

本文提出了一個(gè)被稱(chēng)為分段合并的新的并行原語(yǔ)，實(shí)現(xiàn)了從q個(gè)有序子段到p個(gè)主段的并行合并。這q個(gè)子段的長(zhǎng)度和主段中包含子段的數(shù)目都可以是不同的。我們的主要思想是確定一個(gè)線程所處理的元素?cái)?shù)目，并以二叉樹(shù)的形式將同一段中的子段合并，直到每個(gè)段內(nèi)只剩一個(gè)子段。這種操作可以被廣泛的應(yīng)用于稀疏矩陣的處理中，以解決其中非規(guī)則性導(dǎo)致的負(fù)載不均衡問(wèn)題。在兩個(gè)NVIDIA Turing GPU(RTX 2080和Titan RTX)上進(jìn)行測(cè)試的表明，與NVIDIA cuSPARSE庫(kù)相比，我們的算法使稀疏矩陣轉(zhuǎn)置(SpTRANS)和稀疏矩陣乘法(SpGEMM)運(yùn)算的性能分別提高了3.94和2.89倍。

背景與動(dòng)機(jī)

隨著分段排序、分段掃描、分段求和等并行分段原語(yǔ)的提出和這些分段原語(yǔ)在并行不規(guī)則稀疏矩陣算法上帶來(lái)的良好性能改進(jìn)，分段操作受到了研究人員的廣泛關(guān)注。然而盡管合并算法是計(jì)算機(jī)科學(xué)重要的基礎(chǔ)算法之一，分段合并卻還沒(méi)有受到人們的關(guān)注。基于我們對(duì)稀疏矩陣操作的觀察，分段合并原語(yǔ)可能在稀疏矩陣轉(zhuǎn)置(SpTRANS)和稀疏矩陣乘法(SpGEMM)等操作中很有價(jià)值。因此，我們?cè)诒竟ぷ髦刑岢隽朔侄魏喜⒃Z(yǔ)，并解決了實(shí)現(xiàn)并行分段合并操作的兩大挑戰(zhàn)：一是段的長(zhǎng)度和子段的長(zhǎng)度不均勻?qū)е碌?/span>負(fù)載均衡問(wèn)題；二是在超大規(guī)模并行的圖形處理器(GPU)上向量化問(wèn)題。

設(shè)計(jì)與實(shí)現(xiàn)

在本文中，我們定義了分段合并原語(yǔ)。

假定我們有一個(gè)鍵值對(duì)數(shù)組S，包含p個(gè)段，

(1)

每個(gè)段包含q_i 個(gè)子段，

(2)

我們可以得到

(3)

每個(gè)子段S_i,j 有n_i,j 個(gè)已經(jīng)根據(jù)關(guān)鍵字排序的鍵值對(duì)。我們的分段合并操作就是讓每個(gè)段內(nèi)的所有鍵值對(duì)按關(guān)鍵字有序排列。

基于這個(gè)定義，我們提出了一個(gè)并行分段合并算法，其主要思想是通過(guò)固定線程處理的元素?cái)?shù)量解決負(fù)載均衡的問(wèn)題，并以二叉樹(shù)的形式將同一段中的子段兩兩合并，直到所有子段合并完成。該算法包括三個(gè)步驟：

(1)數(shù)據(jù)預(yù)處理(4-15行)：首先記錄段和子段的位置，然后為每個(gè)線程固定工作量，最后通過(guò)運(yùn)行標(biāo)準(zhǔn)合并路徑算法的分區(qū)策略為每個(gè)線程收集所處理數(shù)據(jù)的信息；

(2)使用合并路徑合并每個(gè)線程的兩個(gè)子序列(16-18行)；單個(gè)線程已經(jīng)包含執(zhí)行合并操作所需的所有信息，可以有效地合并兩個(gè)有序的子段。而子段的合并操作通常由多個(gè)線程完成，這些線程通過(guò)合并路徑算法進(jìn)行合并子段。首先，將與線程對(duì)應(yīng)的子段中的數(shù)據(jù)進(jìn)行多次比較，以生成用于分割兩個(gè)子段的邊界，然后根據(jù)目標(biāo)矩陣，將兩個(gè)子段中的數(shù)據(jù)按照路徑放入輸出序列中，完成合并操作。算法圖中粉紅色虛線框顯示了兩組子段合并的例子。

(3)迭代合并二叉樹(shù)上的子段(3-21行)：同一段的每一個(gè)子段可視為二叉樹(shù)的一個(gè)葉節(jié)點(diǎn)進(jìn)行合并，可能需要多次迭代。當(dāng)段內(nèi)只有一個(gè)子段時(shí)，迭代結(jié)束，分段合并完成。

下圖展示了使用分段合并算法將八個(gè)子段合并為三個(gè)有序段的一個(gè)例子。

分段合并實(shí)例圖

實(shí)驗(yàn)結(jié)果

本文在兩個(gè)NVIDIA Turning GPU(RTX 2080和Titan RTX)上對(duì)SpTRANS和SpGEMM進(jìn)行了測(cè)試，并將它們與NVIDIA 的cuSPARSE v10.2庫(kù)中的相應(yīng)函數(shù)進(jìn)行了比較，數(shù)據(jù)集從SuiteSparse Matrix Collection中進(jìn)行選擇。

我們的SpTRANS算法是將CSR格式的矩陣轉(zhuǎn)置成CSR格式的矩陣。經(jīng)測(cè)試，我們的算法在兩個(gè)GPU上對(duì)于cuSPARSE算法平均加速比分別達(dá)到3.55倍(最高9.64倍)和3.94倍(最高13.09倍)。

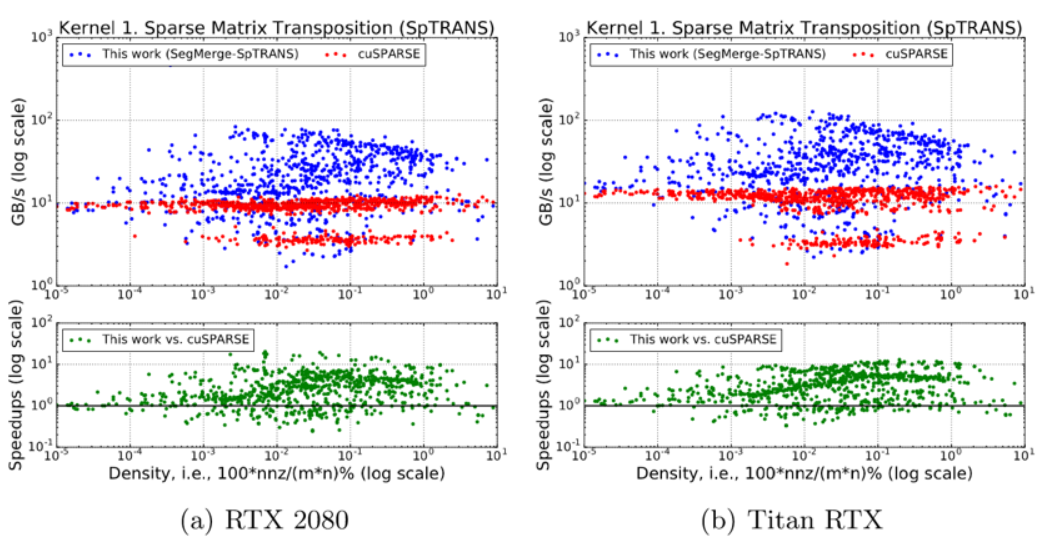
SpTRANS實(shí)驗(yàn)： cuSPARSE方法和使用分段合并原語(yǔ)方法在兩個(gè)NVIDIA GPU上的比較。x軸表示被測(cè)矩陣的密度(非零元數(shù)與行數(shù)和列數(shù)之積的比率)。

SpGEMM算法計(jì)算C=AB，其中A、B和C三個(gè)矩陣都是稀疏的。我們使用行-行方法，每個(gè)處理單元遍歷A行中的非零元，并使用這些值乘以B對(duì)應(yīng)行的所有元素，然后將乘后的元素合并到C的行中。經(jīng)測(cè)試，我們的算法在RTX 2080上，對(duì)于cuSPARSE和bhSPARSE算法平均加速比分別達(dá)到了2.89x(最高109.15x)和1.26x(最高7.5x)；在Titan RTX上，平均加速分別為2.53倍(高達(dá)81.85倍)和1.22倍(最高17.38倍)。

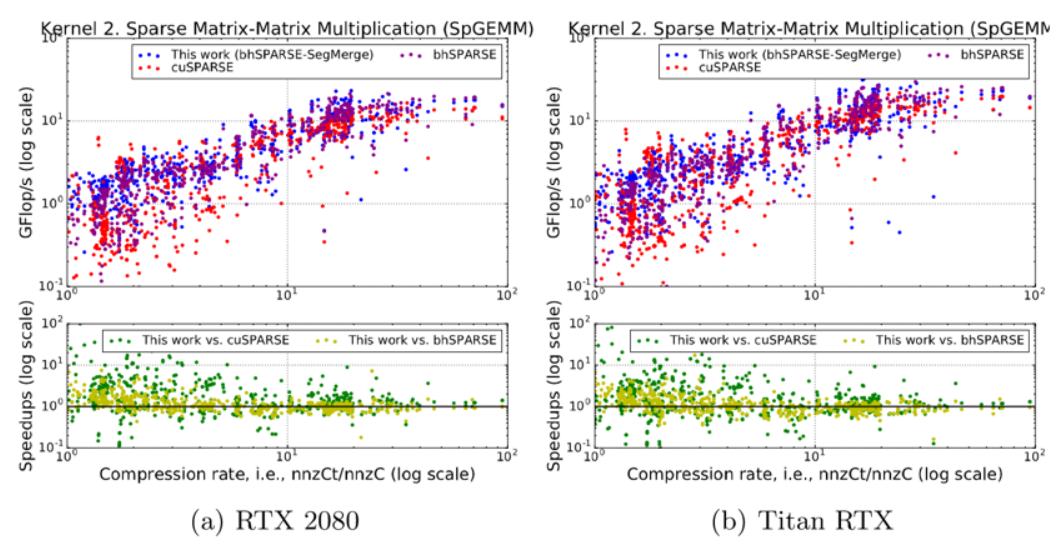
SpGEMM實(shí)驗(yàn)： cuSPARSE方法，bhSPARSE方法和采用分段合并方法在兩個(gè)NVIDIA GPU上的比較。x軸是壓縮率，即結(jié)果矩陣中中間非零元與非零元的數(shù)量之比。

關(guān)于作者：

劉偉峰，博士，中國(guó)石油大學(xué)(北京)信息科學(xué)與工程學(xué)院教授，院長(zhǎng)，歐盟瑪麗居里學(xué)者。2002年和2006年于中國(guó)石油大學(xué)(北京)計(jì)算機(jī)系獲學(xué)士與碩士學(xué)位，2006年至2012年在中國(guó)石化石油勘探開(kāi)發(fā)研究院歷任助理工程師、工程師和高級(jí)研究師，其間主要研究領(lǐng)域?yàn)槭偷厍蛭锢砜碧降母咝阅芩惴ā?/span>2016年于丹麥哥本哈根大學(xué)獲計(jì)算科學(xué)博士學(xué)位，主要研究方向?yàn)楦咝阅芟∈杈€性代數(shù)子程序。他的主要研究興趣為數(shù)值線性代數(shù)和并行計(jì)算，其中尤其關(guān)注稀疏矩陣的數(shù)據(jù)結(jié)構(gòu)、并行算法和軟件。 他的研究工作發(fā)表于SC、ICS、PPoPP、ASPLOS、IPDPS、JPDC、FGCS和Parco等重要國(guó)際會(huì)議和期刊。他還是TPDS、SISC和TKDE等多個(gè)重要國(guó)際期刊審稿人，也是SC、ICS和ICPP等多個(gè)重要國(guó)際會(huì)議的程序委員會(huì)委員。他是IEEE和CCF高級(jí)會(huì)員以及ACM和SIAM會(huì)員。聯(lián)系方式：weifeng.liu@cup.edu.cn